背景
振动信号是指物体在某一参考点附近运动时产生的信号,通常由一个或多个周期性变化的物理量(如位移、速度、加速度等)组成。这些物理量随时间的变化呈现出规律性的重复模式,形成了振动信号的特征
特点
周期性:振动信号具有明确的周期性,即信号会规律性地重复。
频率:振动信号的频率指每秒钟发生的周期数,频率越高,变化速度越快。
幅值:振动信号的幅值表示信号在一个周期内的最大偏离程度,用来表示振动信号的强度。
波形:描述了信号随时间的变化规律,常见的波形包括正弦波、方波、锯齿波等。
傅里叶变换
简介
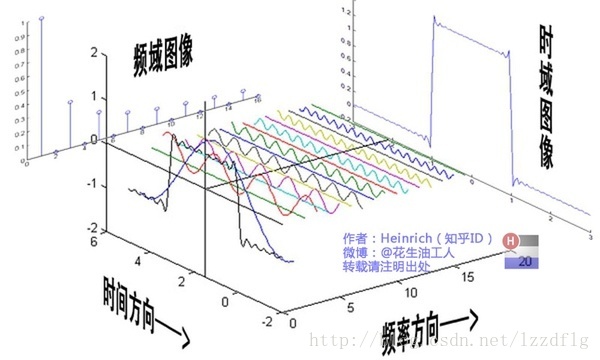
傅里叶变换(Fourier Transform)是一种将时间或空间上的信号转换为频率域上的表示的数学方法。它允许我们分析信号的频率成分。傅里叶变换基于傅里叶级数,可以表示为连续信号的傅里叶变换或离散信号的离散傅里叶变换(DFT)。
优点
频域分析:能够清晰地展示信号的频率成分。
去噪:可以去除特定频率的噪声。
信号压缩:在频域内可以进行信号压缩。
数学性质:具有丰富的数学性质,便于进行数学处理。
缺点
时频分辨率:时间分辨率和频率分辨率不能同时很高。
非局部化:无法提供信号的局部信息。
对突变信号敏感:对于突变或不连续的信号,傅里叶变换的效果不佳。
应用特点
音频分析:分析音频信号的频率成分。
图像处理:用于图像的频率分析和图像压缩。
振动分析:用于机械振动的频率分析。
Python代码实现
import numpy as np
import matplotlib.pyplot as plt
# 创建一个示例信号,例如一个正弦波
fs = 1000 # 采样频率(Hz)
T = 1 # 信号的周期(秒)
N = 1000 # 采样点数
t = np.linspace(0, N-1, N, endpoint=False) / fs # 时间向量
# 创建一个频率为5Hz的正弦波
freq = 5 # 信号频率(Hz)
signal = np.sin(2 * np.pi * freq * t)
# 计算快速傅里叶变换
fft_result = np.fft.fft(signal)
# 获取频率域的频率值
freqs = np.fft.fftfreq(N, 1/fs)
# 绘制原始信号
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('Original Signal')
plt.xlabel('Time [s]')
plt.ylabel('Amplitude')
# 绘制频谱图
plt.subplot(2, 1, 2)
plt.stem(freqs, np.abs(fft_result), 'b', markerfmt=" ", basefmt="-b")
plt.title('Spectrum')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Amplitude')
plt.xlim([0, fs/2]) # 限制x轴显示到Nyquist频率
plt.tight_layout()
plt.show()小波变换
简介
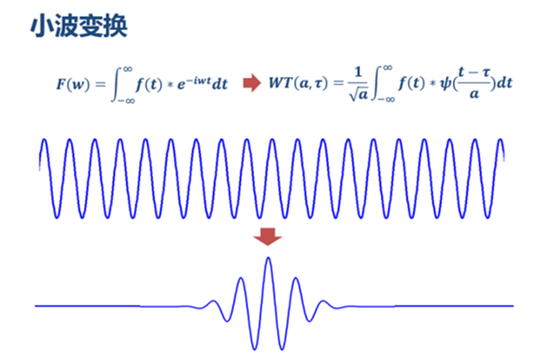
小波变换(Wavelet Transform)是一种时频分析方法,通过将信号投影到一系列称为小波的基函数上,能够同时在时间和频率上提供信号的信息。小波变换特别适合分析非平稳信号,即信号的统计特性随时间变化。
优点
时频局部化:能够提供信号的时频局部化信息。
多尺度分析:通过不同尺度的小波分析信号。
适应性:小波基可以根据信号的特性进行选择或设计。
缺点
计算复杂度:比傅里叶变换的计算复杂度更高。
选择适当的小波基:需要根据具体应用选择合适的小波基。
应用特点
图像去噪:有效去除图像噪声。
特征提取:用于模式识别和机器学习中的特征提取。
数据压缩:用于信号和图像的压缩。
Python代码实现
pip install PyWaveletsimport pywt
import numpy as np
# 创建一个示例信号,例如一个正弦波加上一些噪音
duration = 1.0
sampling_rate = 400
t = np.linspace(0, duration, int(sampling_rate*duration), endpoint=False)
frequency = 5
signal = np.sin(2 * np.pi * frequency * t)
# 添加随机噪音
noise = np.random.randn(len(signal)) * 0.5
noisy_signal = signal + noise
# 选择一个小波基,例如'db1'(Daubechies小波)
wavelet = 'db1'
level = 4 # 小波分解的层数
# 进行小波分解
coeffs = pywt.wavedec(noisy_signal, wavelet, level=level)
# 重构信号
reconstructed_signal = pywt.waverec(coeffs, wavelet)
# 计算小波变换的系数
cA, cD = pywt.dwt(signal, wavelet)小波包变换
简介
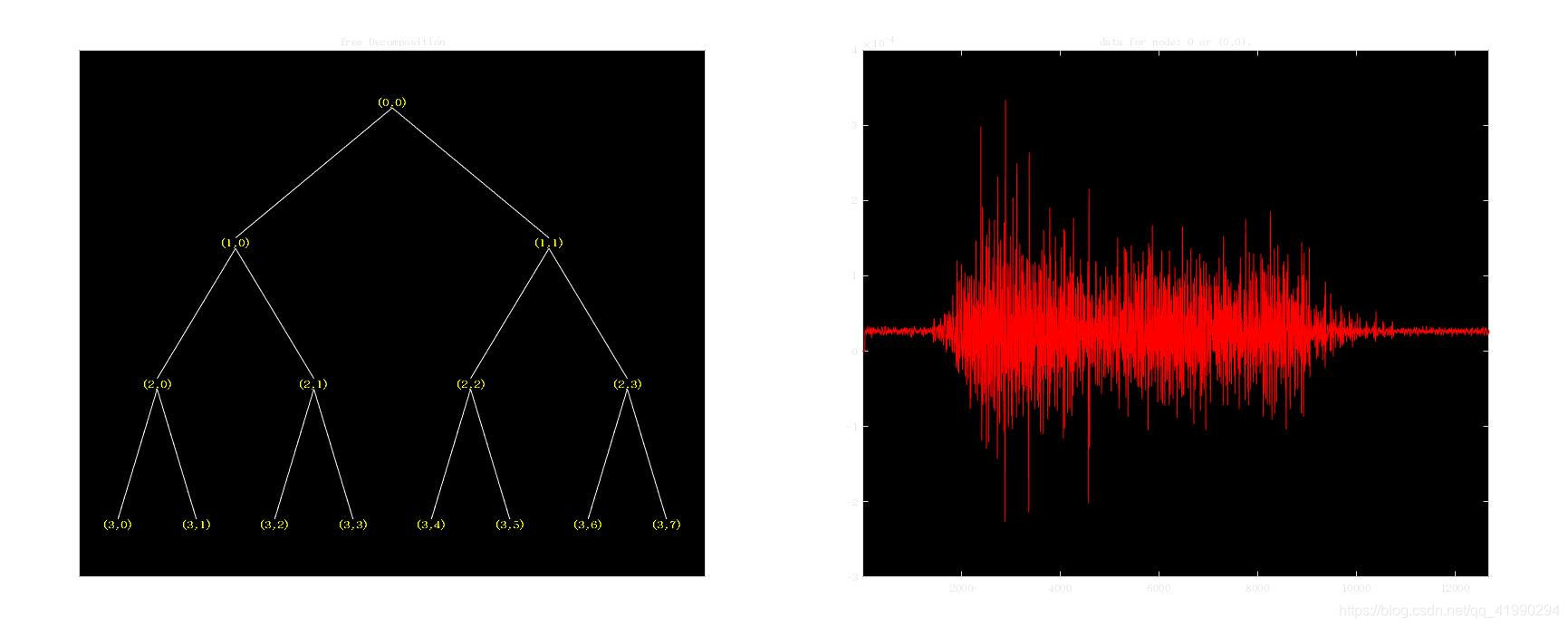
小波包变换(Wavelet Packet Transform)是小波变换的扩展,它不仅将信号分解到不同频率,还对频率分量进行进一步的分解。小波包变换提供了更灵活的信号分析方式,能够适应各种信号的特性。
优点
更高的灵活性:可以对信号的任意频率成分进行分解。
信号分析:能够提供更细致的信号分析。
适应性强:可以根据信号的特性选择最合适的分解方式。
缺点
计算量:比小波变换有更大的计算量。
数据量:分解后的数据量较大,可能导致存储和处理的困难。
应用特点
信号处理:用于复杂信号的分析和处理。
图像分析:用于图像的多尺度分析和特征提取。
数据压缩:用于高效的数据压缩和传输。
Python代码实现
pip install PyWaveletsimport pywt
import numpy as np
# 创建一个示例信号
t = np.linspace(0, 1, num=512)
signal = np.sin(2 * np.pi * 10 * t) + np.sin(2 * np.pi * 20 * t)
# 选择一个小波基,例如'db1'(Daubechies小波)
wavelet = 'db1'
maxlevel = 3 # 最大分解层数
# 创建小波包对象
wp = pywt.WaveletPacket(data=signal, wavelet=wavelet, mode='symmetric', maxlevel=maxlevel)
# 进行小波包分解
wp_max = wp.get_level(maxlevel, 'freq')
# 提取特定节点的数据
node = wp.get_node('aad')
coeffs = node.data
# 从小波包树重构信号
reconstructed_signal = wp.reconstruct(update=True)
# 绘制原始信号和重构信号
import matplotlib.pyplot as plt
plt.figure(figsize=(12, 6))
plt.plot(t, signal, label='Original Signal')
plt.plot(t, reconstructed_signal, label='Reconstructed Signal', linestyle='--')
plt.legend()
plt.show()总结
傅里叶变换、小波变换和小波包变换都是信号处理中的重要工具,它们各自有独特的优势和应用场景。傅里叶变换适用于频域分析,小波变换适合时频局部化分析,而小波包变换提供了更高的灵活性和适应性。在实际应用中,选择哪种变换方法取决于信号的特性和分析的需求。

评论